前言
本篇博客介绍ECCV2016发表的论文 Towards perspective-free object counting with deep learning。 本篇论文同样是利用多个不同尺度的分支一起预测密度图,区别在于多个分支采用同样结构,而为每个分支采样不同尺度的输入。 注:正文包括笔者对原论文的翻译和自己的理解,请读者注意区分人称。
Abstract
在本文中,我们解决了对图像中的对象实例进行计数的问题。我们的模型能够精确地估计交通拥堵中的车辆数量,或在非常拥挤的场景中估计人数。我们的第一个贡献是提出了一种新颖的卷积神经网络解决方案,名为Counting CNN(CCNN)。本质上,CCNN是回归模型,在该模型中,网络学习如何将图像patch映射到其相应的密度图。我们的第二个贡献在于一个尺度计数模型Hydra CNN,它能够在无法提供场景几何信息的非常拥挤的场景中估算密度。Hydra CNN学习了一种多尺度非线性回归模型,该模型使用在多个尺度上提取的图像金字塔来执行密度预测。
Introduction
略
Related Work
略
Method
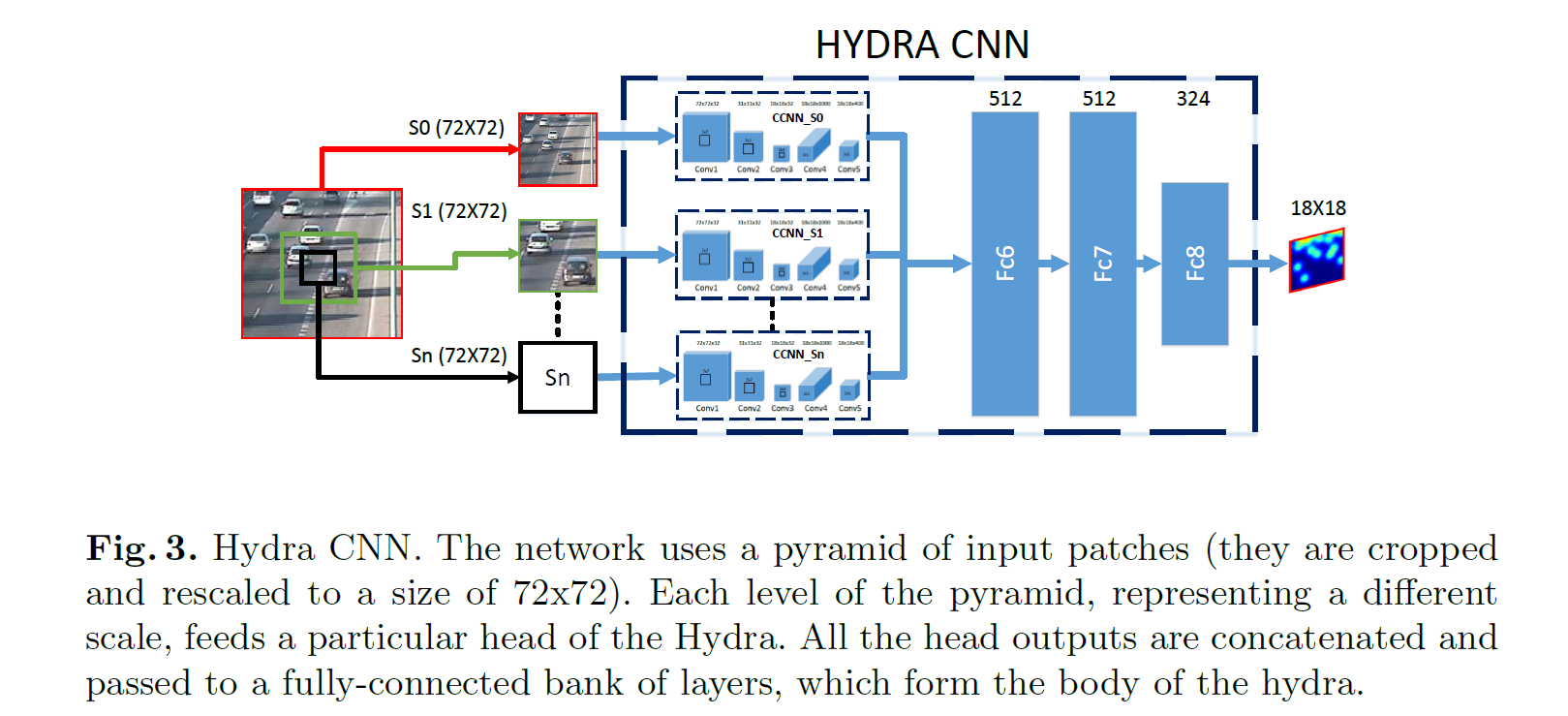
先看一下论文的整体结构:
建模
给定一个输入patch,网络输出其对应密度图,最终多个patch整合为整体结果。
The Counting CNN
这个CCNN的结构没有什么值得解读的,就是一个全卷积结构,作者花了很大篇幅来说明自己与前人工作的不同。看结构:
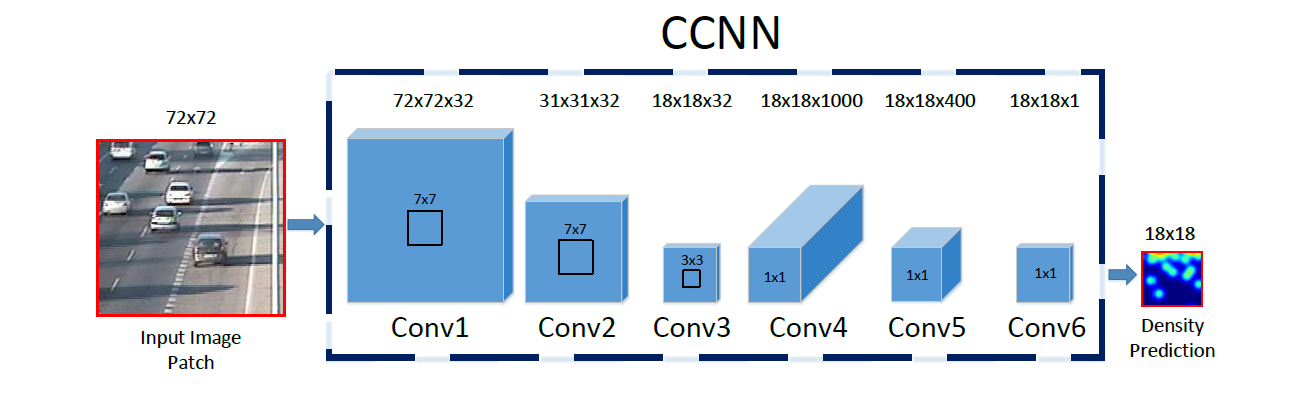
输入的patch都被rescale到$72 \times 72$,由于最终密度图尺度缩小至1/4,所以需要对输出的密度图放大至$72 \times 72$,再对其中的值进行归一化,归一化方式为:
其中$\hat{D}_{\text {pred}}^{P}$是放大之后的密度图。
之后将所有patch的对应结果拼合回去,其中一些像素不止被提取了一次,所以还要再做一次归一化,就是把这个像素位置的值除以它被提取进入patch的次数。
先吐槽一下,本文这一节行文很不正式哈。 然后看一下第二次归一化的细节,恰好前一阵用pytorch实现一个模块的时候用到了。一般取patch的操作使用Unfold操作实现,对每一个patch计算出结果之后,再用Fold函数拼回去,但是需要注意fold(unfold(x)) != x,参见这个issue,这里面用了一种很巧妙的方式做归一化,就是用一个权值都为1的矩阵做和x一样的unfold-fold的过程,根据结果算出每个位置对应的归一化系数:
x = torch.ones(H*W).reshape(1, 1 ,H, W).float()
y = torch.nn.functional.unfold(x, 3, padding=1)
z = torch.nn.functional.fold(y, (H,W), 3, padding=1)
ratio=z/x
Hydra CNN
对于一般的基于回归的计数模型,由于透视效应的干扰,通常需要对输入特征进行 geometric correction。本文通过对输入取金字塔来克服透视干扰。HydraCNN由多个Head和一个几层全连接层构成。每个Head都是一个CCNN,至于后面为什么要用全连接层,原文这里解释的不太清楚,说由于每个Head可以采用不同的结构,导致每个Head输出的特征维度可能不同,用全卷积结构不合适。
每个Head获得的输入都是上文提到的patch的一部分,举例n=3时,也就是回归三个尺度的密度图,
- S0: 整个patch
- S1:在中间抠出面积为2/3的图
- S2:在中间抠出面积为1/3的图
Experiments
略