前言
本篇博客是笔者人群计数读书笔记的第一篇，介绍的工作来源于上海科技大学在CVPR2016发表的论文 MCNN。这是将深度学习应用于人群计数的早期工作之一。 虽然网络结构比较简单，但是适合作为我们进入人群计数领域的基础工作，在这里推荐一个基于pytorch框架的简洁开源实现Github，建议对照学习。 注：正文包括笔者对原论文的翻译和自己的理解，请读者注意区分人称。
Abstract
本文提出了一种在任意人群密度或任意透视关系下准确估计单张图片人群数量的方法。为此，我们提出了一个简单有效的多列卷积神经网络架构来将图片映射为对应的人群密度图。该网络允许输入图片为任意分辨率。通过使用不同尺寸感受野的滤波，每列网络学习到的特征能够适应由于图片分辨率或透视效应导致的人体或头部尺度变化。更进一步地，真值密度图是基于几何自适应核计算的（注：而不是之前工作使用的固定尺寸核），因此无需知道输入图像的透视关系图。由于现有数据集无法足够覆盖我们的方法所考虑到的场景需求，我们收集并标注了一个新的包含1198张图片，330,000个头部标注的的大型数据集。在已有数据集和这个新的困难数据集上我们进行了扩展实验证明了我们方法的有效性。尤其需要指明，我们这个简单的网络超过了全部现有工作。同时，我们证明了我们的模型一旦在一个数据集上训练好，可以轻易地迁移到新的数据集。
Introduction
在2015年的新年夜，35人在中国上海的一场拥挤踩踏事故中遇难。不幸的是，自那以后，更多的拥堵事故发生在全球各地造成更严重的伤亡。因此从图片中或视频中准确估计拥挤情况变成愈加重要的计算机视觉应用以助于拥堵控制和公众安全。在一些场景下，例如公众集会和运动盛会，参与人数或人群密度对于未来举办规划和场地设计是很重要的信息。好的人群计数的方法还可以延伸到其他领域，例如，从显微图像中查出细胞或细菌数量，野生动物保护区内动物数量估计，或者在交通枢纽或交通拥挤处估计机动车数量。
Related Work
许多文献已经提出了一些人群计数的算法。早期工作采用检测式框架扫描跨视频连续帧的检测器来估计行人数量，这些检测器是基于集成了外观和运动特征的。还有一些工作（注：这里的引用文章请参考原文引用）使用了类似的基于检测的框架。在这些方法中，研究者通常假设人群是由独立的个体组成的，这些个体可以被一些现有的检测器检测，这些方法的局限之处在于，在一些聚集环境或者特别密集的拥挤环境中，遮挡严重影响了检测器准确性，进而影响最终行人数量估计的准确性。
在视频中的人群计数中，人们提出了对视觉特征的追踪轨迹据类的方法，但是这一类方法不适用于独立的静止图片。
可以说最被广泛使用的方法是基于特征的回归方法。这一类方法的主要步骤是：1）分割前景2）从前景中提取不同特征，例如人群面积，边缘检测，纹理特征。3）利用一个映射函数进行数值的回归，线性函数或者分段线性函数可以取得不错的性能，其他高级的或更有效的回归方法例如岭回归，高斯过程回归或者神经网络也被使用。
一些专门针对静态图像的人群计数方法也被提出。比如一些方法利用不同信息–兴趣点，傅里叶分析，小波分解等特征融合进行预测。还有近期一些基于CNN的方法也出现了。虽然这些方法在已有数据中取得较好结果，但是这些方法都需要训练数据和测试数据的透视关系，实际上在应用场景中却很难获得，因此限制了这些方法的应用价值。
Contributions of this paper
在本文中，我们旨在从任意静止图像，摄像机视角和人群密度进行准确的人群计数。乍一看，这似乎是一项艰巨的任务，因为我们显然需要克服一系列挑战：
- 在大多数现有工作中，前景分割是必不可少的。 然而，前景分割本身就是一项具有挑战性的任务，不正确的分割将对最终计数产生不可逆的不利影响。 在我们的任务中，图像的视角可以是任意的。 没有有关场景几何或运动的信息，几乎不可能从人群的背景中准确地分割出人群。 因此，我们必须在不先分割前景的情况下估计人群的数量。
- 在我们的任务（或数据集）中，人群的密度和分布差异很大，通常每个图像中的大多数人都有严重的遮挡。因此，传统的基于检测的方法不适用于此类图像和情况。
- 由于图像中人物的比例可能存在很大差异，因此我们需要一起使用不同比例的特征，以便准确估计不同图像的人群数量。 由于我们没有跟踪的视觉特征，并且很难手工提取所有不同比例的特征，因此我们不得不求助于能自动学习有效特征的方法。
为了克服上述挑战，我们提出了一种基于卷积神经网络的新框架，用于在任意静止图像中进行人群计数。具体来讲，我们提出了一种多列卷积神经网络（MCNN）。 我们的MCNN包含三列卷积神经网络，它们的滤波大小不同。 MCNN的输入是图像，输出是人群密度图，其积分为总体人群数。
注：值得注意的是，MCNN的网络架构来源于 Jurgen Schmidhuber,也就是LSTM的创造者在2012年发表的论文MCDNN, ，联想到他在2019年底发表的万字长文，阐述深度学习的各项成就“皆备于我”，参见「LSTM 之父」亲笔万字长文，只为向世人证明：深度学习不是在母语为英语的地方被发明的，看来还真是言之不虚啊哈哈。
本文的贡献总结如下：
- 我们采用多列架构的原因是很自然的：三列对应于具有不同大小（大，中，小）感受野的滤波，因此每列CNN所学习的特征都适用于因透视效应或不同分辨率而导致的人/头大小的较大变化。
请各位读者记住这个结论，但是不要把它作为金科玉律，在后续CSRNET的解读中我们会看到这条结论也许太过“仓促”。
- 在我们的MCNN中，我们将全连接层替换为为1×1的卷积层。因此，模型的输入图像可以具有任意大小以避免失真。网络的直接输出是对人群密度的估计，从中可以得出总体计数。
这个优点实际上会在代码实现上产生一个问题：采用默认的dataloader,batchsize只能为1,(因为输入图片大小不一)，网络中也无法使用BN层。不过有以下几种解决方法：
- 改写dataloader的collect_fn函数，对输入图像加padding，使其大小一致。
- 改写dataloader的collect_fn函数，将输入图像crop至batch中最小宽高。
- 通过在网络开始阶段添加AdaptivePool操作，使其在后续阶段成为统一尺寸。
实际上，在$C^3$ Framework技术报告中提到:“根据经验，如果是from scratch training，对于这几个数据集建议采用多batch size训练或者采用GCC-SFCN中加padding的方案，对于有预训练参数的模型（AlexNet，VGG，ResNet等），建议采用单一batch size进行训练。”
- 我们收集了一个新的数据集，用于评估人群计数方法的性能。
现有的人群计数数据集无法在本工作考虑的各种场景中全面测试算法的性能，因为它们在视角变化（UCSD，WorldExpo’10），人群规模（UCSD），数据集规模（UCSD，UCF CC 50）方面存在局限性或各种场景（UCF CC 50）。 在这项工作中，我们介绍了一个名为Shanghaitech的新的大规模人群数据集，其中包含近1200张图像和约330,000个准确标记的头部。据我们所知，就人数标注数量而言，它是最大的人群计数数据集。 该数据集由两部分组成：A部分和B部分。A部分中的图像是从Internet上随机爬取的，其中大部分图像中人群密度较大。 B部分取自上海大都市的繁忙街道。
Multi-column CNN for Crowd Counting
Density map based crowd counting
用卷积神经网络（CNN）估计给定图像中的人数，有两种配置方式。 一个输入图像输出人数（数字形式）。另一种是输出人群的密度图（例如每平方米有多少人），然后通过积分获得人数。 在本文中我们选择第二种：
- 密度图保留了更多信息。
与人群总数相比，密度图给出了给定图像中人群的空间分布，这种分布信息在许多应用中很有用。例如，如果某区域的密度比其他区域的密度高得多，则可能表明那里发生了异常情况。 - 在通过CNN学习密度图时，所学习的滤波器更适合于不同大小的头部大小，因此更适合于透视效果显著变化的任意输入。因此，滤波器在语义上更具意义，因此提高了人群计数的准确性。
Density map via geometry adaptive kernels
由于需要对CNN进行训练以从输入图像中估计人群密度图，因此训练数据中给出的密度质量在很大程度上决定了我们方法的性能。 我们首先描述如何将带有标签人头的图像转换为人群密度图。
如果在像素$x_i$处有头部，则将其表示为增量函数$\delta(x-x_i)$。
因此，带有N个头部标记的图像可以表示为函数$H(x)= \sum\limits_{n=1}^N\delta(x-x_i)$。
为了将其转换为连续密度函数，我们可以将该函数与高斯核$G_\sigma$卷积，以使密度为$F(x)= H(x)*G_\sigma(x)$。
但是，这种密度函数假定这些$x_i$是图像平面中的独立样本，实际上，这些$x_i$是一个3D场景中的样本，并且由于透视效应，这样标注密度图是不合理的。
这里没理解:In fact, each $x_i$ is a sample of the crowd density on the ground in the 3D scene and due to the perspective distortion, and the pixels associated with different samples $x_i$ correspond to areas of different sizes in the scene.
因此，为了准确估计人群密度$\mathrm{F}$，我们需要考虑由地平面和像平面之间的单应性引起的失真。
单应性(homography)变换用来描述物体在两个平面之间的转换关系，是对应齐次坐标下的线性变换。即$X’=H \cdot X$。例如我们可以通过物理变换矩阵和相机内参数矩阵来映射平面图像上的点和三维空间点坐标。
不幸的是，对于现有的任务（和数据集），我们通常不知道场景的几何信息。但是，如果我们假设每个头部周围的人群分布都比较均匀，则头和它的最近k个邻居之间的平均距离可以合理估计由透视效应引起的几何失真。 因此，我们应该基于图像中每个人的头部大小来确定尺度参数$\sigma$。然而，实际上，在许多情况下，由于遮挡，几乎不可能准确地获得头部的大小，并且也很难找到头部大小与密度图之间的潜在关系。有趣的是，我们发现头的大小通常与拥挤场景中两个相邻人的中心之间的距离有关。作为一种折衷，对于那些拥挤场景的密度图，我们提出根据每个人与邻居的平均距离来自适应地确定每个人的尺度参数。
原文注：对于给定密度图或透视图的输入图像，我们在实验中直接使用给定的密度图或使用从透视图生成的密度图。对于仅包含很少的人，并且头部大小相似的输入图像，我们对所有人使用固定的尺度参数。其余情况下我们采用上述基于KNN方法生成的密度图。
这里我们暂停一下，结合代码理解一下这种密度图的生成方式。
def gaussian_filter_density(img,points):
"""
This code use k-nearst, will take one minute or more to generate a density-map with one thousand people.
points: a two-dimension list of pedestrians' annotation with the order [[col,row],[col,row],...].
img_shape: the shape of the image, same as the shape of required density-map. (row,col). Note that can not have channel.
return:
density: the density-map we want. Same shape as input image but only has one channel.
example:
points: three pedestrians with annotation:[[163,53],[175,64],[189,74]].
img_shape: (768,1024) 768 is row and 1024 is column."""
img_shape=[img.shape[0],img.shape[1]]
print("Shape of current image: ",img_shape,". Totally need generate ",len(points),"gaussian kernels.")
density = np.zeros(img_shape, dtype=np.float32)
gt_count = len(points)
if gt_count == 0:
return density
leafsize = 2048
# build kdtree
tree = scipy.spatial.KDTree(points.copy(), leafsize=leafsize)
# query kdtree
distances, locations = tree.query(points, k=4)
#这里使用KDTree是加快KNN查询速度，可以将
print ('generate density...')
for i, pt in enumerate(points):
pt2d = np.zeros(img_shape, dtype=np.float32)
if int(pt[1])<img_shape[0] and int(pt[0])<img_shape[1]:
pt2d[int(pt[1]),int(pt[0])] = 1.
else:
continue
if gt_count > 1:
sigma = (distances[i][1]+distances[i][2]+distances[i][3])*0.1
#KNN,K=3
else:
sigma = np.average(np.array(gt.shape))/2./2. #case: 1 point
density += scipy.ndimage.filters.gaussian_filter(pt2d, sigma, mode='constant')
#以当前点为中心生成高斯分布，叠加到密度图上。
print ('done.')
return density
所以最终密度图生成方式为：
$F(x)=\sum_{i=1}^{N} \delta(x-x_{i}) * G_{\sigma_{i}}(x), \quad with \quad \sigma_{i}=\beta \bar{d}^{i}$
原文中说$\beta$取0.3效果最好，上面的代码中0.1是因为K=3时求距离均值除以3和0.3约分。
Multi column CNN for density map estimation
由于透视失真，图像通常包含大小各异的头部，因此具有相同大小的感受野的滤波不太可能捕获不同比例的人群密度特征。
因此，使用具有不同大小的局部感受野的滤波器来学习从原始像素到密度图的映射是更自然的。受多列深度神经网络（MDNN）成功的启发，我们提出使用多列CNN（MCNN）来学习目标密度图。
在我们的MCNN中，对于每一列，我们使用不同大小的滤波器来建模与不同比例的头部相对应的密度图。例如，具有较大感受野的滤波对于建模对应于较大头部的密度图更为有用。
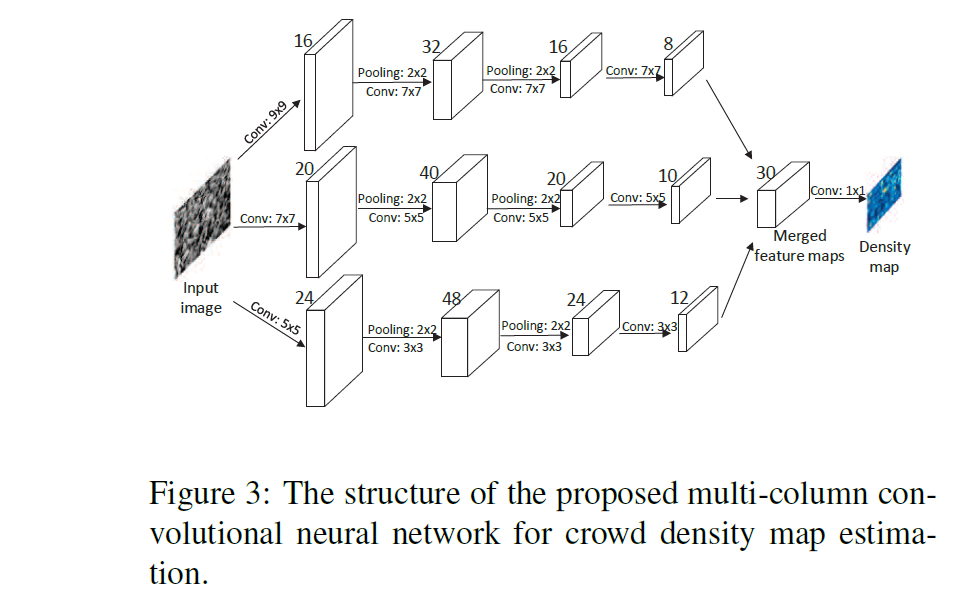
我们的MCNN的整体结构如图3所示。它包含三个并行的CNN，它们具有不同的感受野。 为了简化，我们对所有列使用相同的网络结构（conv-pooling-conv-pooling），除了滤波器的大小和数量。 最大池化核大小为2，采用（ReLU）作为激活函数。 为了降低计算复杂度（要优化的参数数量），
实际上参数量和计算复杂度还是有一定区别的
对于具有较大滤波的CNN，我们使用较少的滤波器数量。
论文里用的是filter，所以我一直翻译成滤波,其实就是不同列使用不同大小的卷积核，对于大卷积核分支，减少对应的通道数。
我们concat所有CNN的输出特征图，并用$1 \times 1$卷积将它们映射到密度图。然后，使用欧氏距离作为损失函数。
原文备注：i）由于我们使用两层最大池化，因此特征图分辨率降低为$1/4$。因此，在训练阶段，在生成密度图之前，我们还将训练样本降低为$1/4$分辨率。 ii）传统的CNN通常将其输入图像归一化为相同大小。在这里，我们保持输入图像的原始大小，因为将图像调整为相同大小会在密度图中引入额外的失真。 iii）除了CNN的卷积核大小不同外，我们的MCNN与传统MDNN的另一个区别是我们将所有CNN的输出结合了可学习的权重（即1×1过滤器）。 相反，在MDNN中，仅对输出进行平均。
Optimization of MCNN
损失函数可以通过批随机梯度下降和反向传播进行优化。 但是，实际上，由于训练样本的数量非常有限，并且由于梯度消失现象的影响，因此同时学习所有参数并不容易。
受RBM预训练的影响，我们通过直接将第四卷积层的输出映射到密度图来分别对每个单列中的CNN进行预训练。 然后，我们使用这些经过预训练的CNN来初始化所有列中的CNN，并同时微调所有参数。
Transfer learning setting
MCNN模型的一个优点是，学习到了不同头部大小的建模信息。 因此，如果在包含不同大小的头部的大型数据集上训练模型，则可以轻松地将模型迁移到其他头部具有某些特定大小的数据集。 如果目标域仅包含少量训练样本，则可以简单地在MCNN中固定每列中的前几层，并仅微调后几层卷积层。 在这种情况下，微调最后几层有两个优点。 首先，通过固定前几层，可以保留在源域中学习的知识，并且通过对后几层进行微调，可以使模型适应目标域。 因此，源领域和目标领域的知识都可以集成在一起，并有助于提高准确性。 其次，与微调整个网络相比，微调最后几层大大降低了计算复杂度。
Experiments
具体实验结果省略，看一下发布的数据集Shanghaitech dataset吧。
Shanghaitech dataset
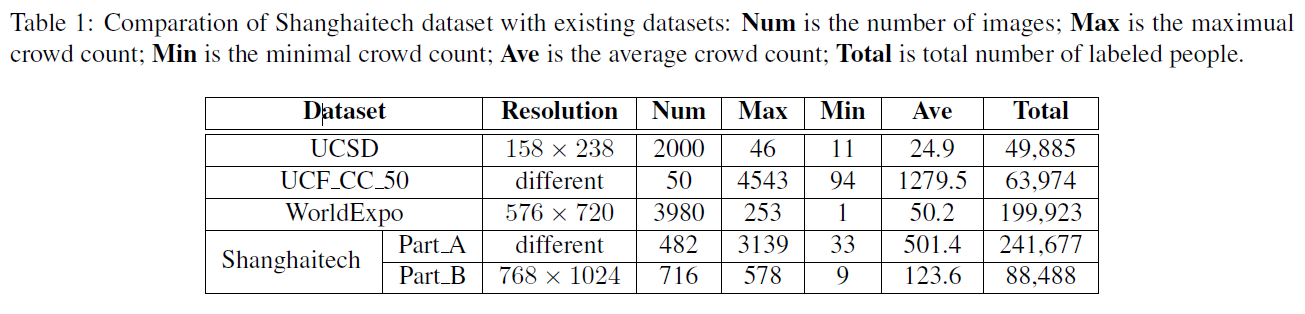
我们引入了一个名为Shanghaitech的新的大规模人群计数数据集，其中包含1198幅带注释的图像，总共330,165人的头部中心注释。 据我们所知，就注释人的数量而言，该数据集是最大的数据集。 该数据集由两部分组成：A部分中有482张图像，是从Internet上随机抓取的，B部分中有716张图像，是从上海市的繁忙街道上拍摄的。 两个子集的人群密度存在显著变化，这使得人群的准确估计比大多数现有数据集更具挑战性。 A部分和B部分都分为训练和测试：A部分的300张图像用于训练，其余182张图像用于测试； B部分的400张图像用于训练，316张用于测试。 表1给出了Shanghaitech数据集的统计数据及其与其他数据集的比较。
另外还有一个比较有趣的实验是比较单列CNN与多列CNN的性能。
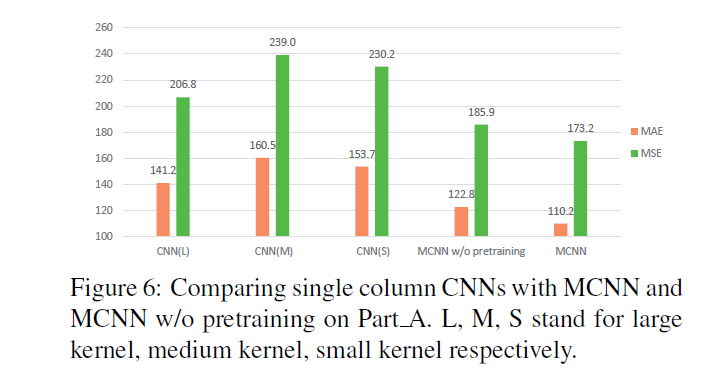图6显示了Shanghaitech A上单列CNN与MCNN的比较。可以看出，对于MAE和MSE，MCNN明显优于每个单列CNN。这验证了MCNN结构的有效性。
这个实验验证的是将单列CNN分别单独训练的性能和MCNN使用这些单列CNN作为预训练的性能，以及MCNN从头开始训练的性能，可以看到几个单列CNN的性能是比较接近的(CSRNet的伏笔),MCNN性能总是优于单列CNN。预训练的MCNN优于从头开始训练的，这一点比较好理解，可以类比一下HourGlass网络中的中间监督，对网络每一个独立组件引入监督信息，使其变为一个集成学习器。
MCNN是深度学习应用 于人群计数早期文章之一，至今仍然会被最新的论文在实验里引用23333,我们在阅读这类开创期论文的时候不要觉得它太简单，要注意其中出现的分析论断，在后续阅读其他论文时看一看哪些想法成为了领域主流，哪些想法被推翻，哪些想法还不够成熟，这样才能发掘出新的想法，（才能水论文）。